Stel je voor: je staat ergens in Nederland met een GPS in je hand. Die toont je locatie in graden en minuten – maar ergens in een kantoor van het Kadaster wordt diezelfde plek aangeduid met coördinaten als 155.000, 463.000. Welkom in de wereld van het Rijksdriehoekstelsel, een van de meest ingenieuze en nauwkeurige coördinatenstelsels ter wereld.

Het begin: de droom van de perfecte kaart

Ons verhaal begint aan het einde van de 18e eeuw, in een tijd van revolutie en wetenschappelijke vooruitgang. In Frankrijk werkten de knapste koppen aan een project dat de wereld zou veranderen: het exact opmeten van de aarde. Wiskundigen als Pierre-Simon Laplace legden de basis voor de moderne geodesie: de wetenschap van het nauwkeurig meten van de aarde. Hun doel: een gestandaardiseerd, betrouwbaar systeem, essentieel voor administratie, belastingen en natuurlijk militaire strategie, een obsessie van de latere keizer Napoleon.

Hier krijgt ons verhaal een Nederlandse wending. Onder invloed van deze Franse ontwikkelingen kreeg de Nederlandse arts, generaal en wetenschapper Cornelis Krayenhoff rond 1800 de opdracht van de toenmalige Bataafse Republiek om heel Nederland voor het eerst systematisch in kaart te brengen. Gewapend met de revolutionaire Franse meettechnieken, de modernste theodolieten en een ongekende precisiedrang, begon hij aan een mammoetproject.

De geboorte van de driehoek

Krayenhoff en zijn team stonden voor een enorme uitdaging: hoe karteer je een land dat zo vlak, drassig en uitgestrekt is? Hoe meet je afstanden over polders, rivieren en heidevelden?

Hun oplossing was zo elegant dat we hem vandaag de dag nog steeds gebruiken: triangulatie. In plaats van het hele land meter voor meter op te meten, kozen ze strategische, hoge punten (zoals kerktorens) en maten ze uiterst precies de hoeken tussen die punten. De rest? Dat rekenden ze uit.

Het principe is verrassend eenvoudig. Als je de lengte kent van één zijde van een driehoek (de basislijn), en je meet de hoeken naar een derde punt, kun je met trigonometrie feilloos de lengte van de andere zijden en de exacte positie van dat derde punt berekenen. Vanaf dat nieuwe punt maak je weer nieuwe driehoeken, en zo weef je een onzichtbaar web van precisie over het hele land.

De wiskunde achter de magie

Voor de wiskundige zielen onder ons: het hart van de driehoeksmeting is de sinusregel:

Hierbij stellen we:

• $BC$ de afstand tussen torens B en C
• $AC$ de afstand tussen torens A en C
• $AB$ de afstand tussen torens A en B

Stel, je weet de afstand tussen kerktoren A en kerktoren B: ? m. Vanaf toren A en B meet je de hoeken die de torens aan de horizon maken:

• Hoek bij toren A: ?°
• Hoek bij toren B: ?°

Met deze gegevens kun je exact uitrekenen waar toren C ligt, zonder deze ooit te beklimmen. De ontbrekende hoek bij toren C volgt uit het feit dat de hoeksom van een driehoek altijd 180° is:

Zodra alle hoeken bekend zijn, kunnen deze waardes en de afstand tussen torens A en B in de formule invullen:

Van chaos naar systeem: het moderne RD-stelsel

Het netwerk van Krayenhoff was een meesterwerk voor zijn tijd. Maar na een eeuw van gebruik en nieuwe inzichten, werd in de vroege 20e eeuw besloten dat het tijd was voor een compleet nieuw, wiskundig zuiverder systeem. Hoe zorg je ervoor dat al die duizenden driehoeken één consistent, nationaal geheel vormen?

De oplossing was een centraal referentiepunt. Voor Nederland werd gekozen voor de Onze-Lieve-Vrouwetoren in Amersfoort. De reden? Simpel: het is de meest centrale kerktoren van het land.

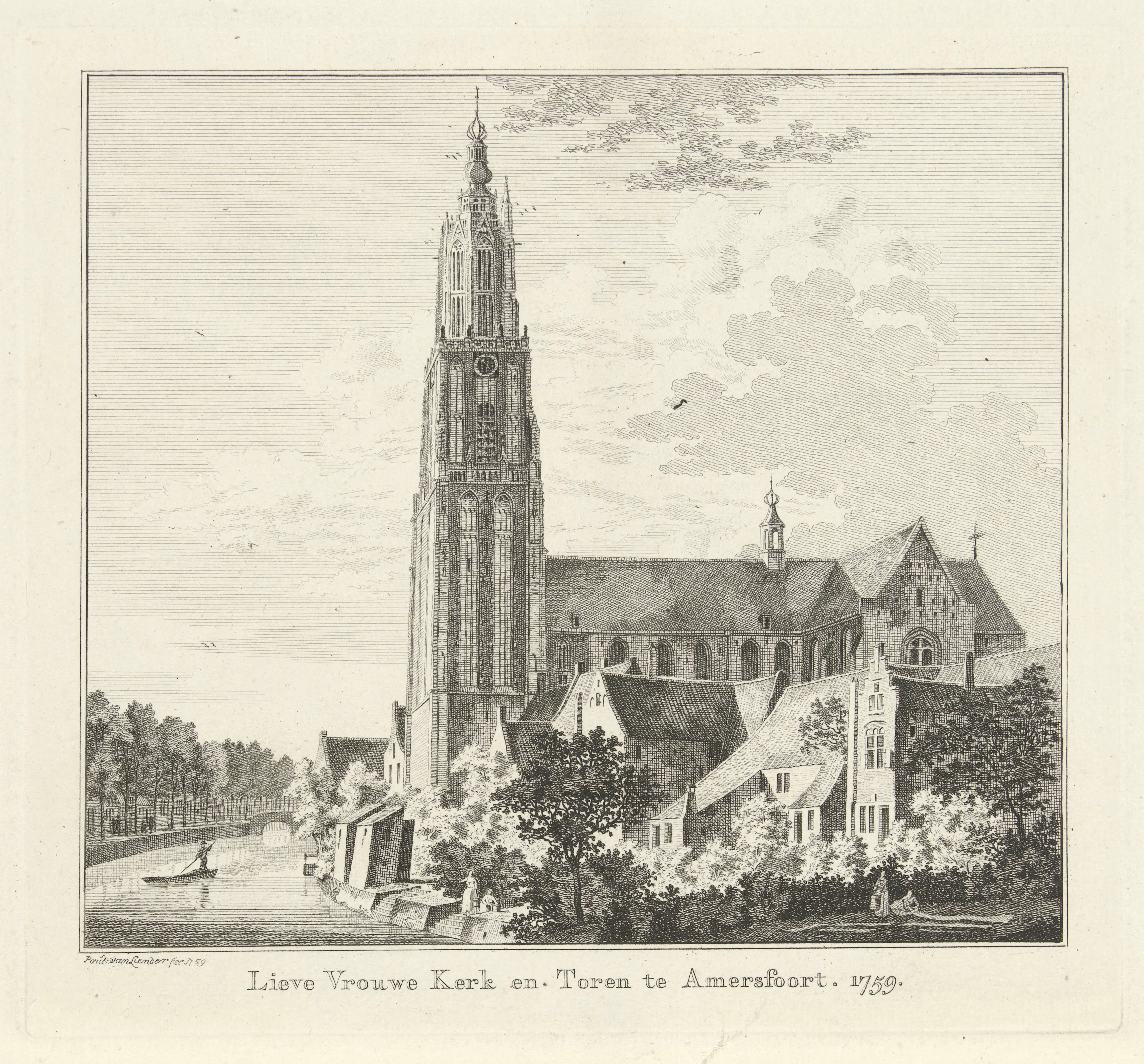
Pas rond 1930 kreeg dit punt, na jaren van complexe berekeningen, zijn nu beroemde coördinaten: X=155.000, Y=463.000. Die getallen lijken willekeurig, maar zijn slim gekozen zodat alle coördinaten in Nederland positief zijn en de getallen niet onnodig groot worden. Dit was de geboorte van het moderne Rijksdriehoekstelsel.

Waarom RD nog steeds beter is dan GPS (voor Nederland)

Fast forward naar de 21e eeuw. Waar Krayenhoff met telescopen op kerktorens klom, hebben we nu GPS-satellieten die tot op de centimeter nauwkeurig zijn. Toch gebruiken we nog steeds het Rijksdriehoekstelsel. Waarom?

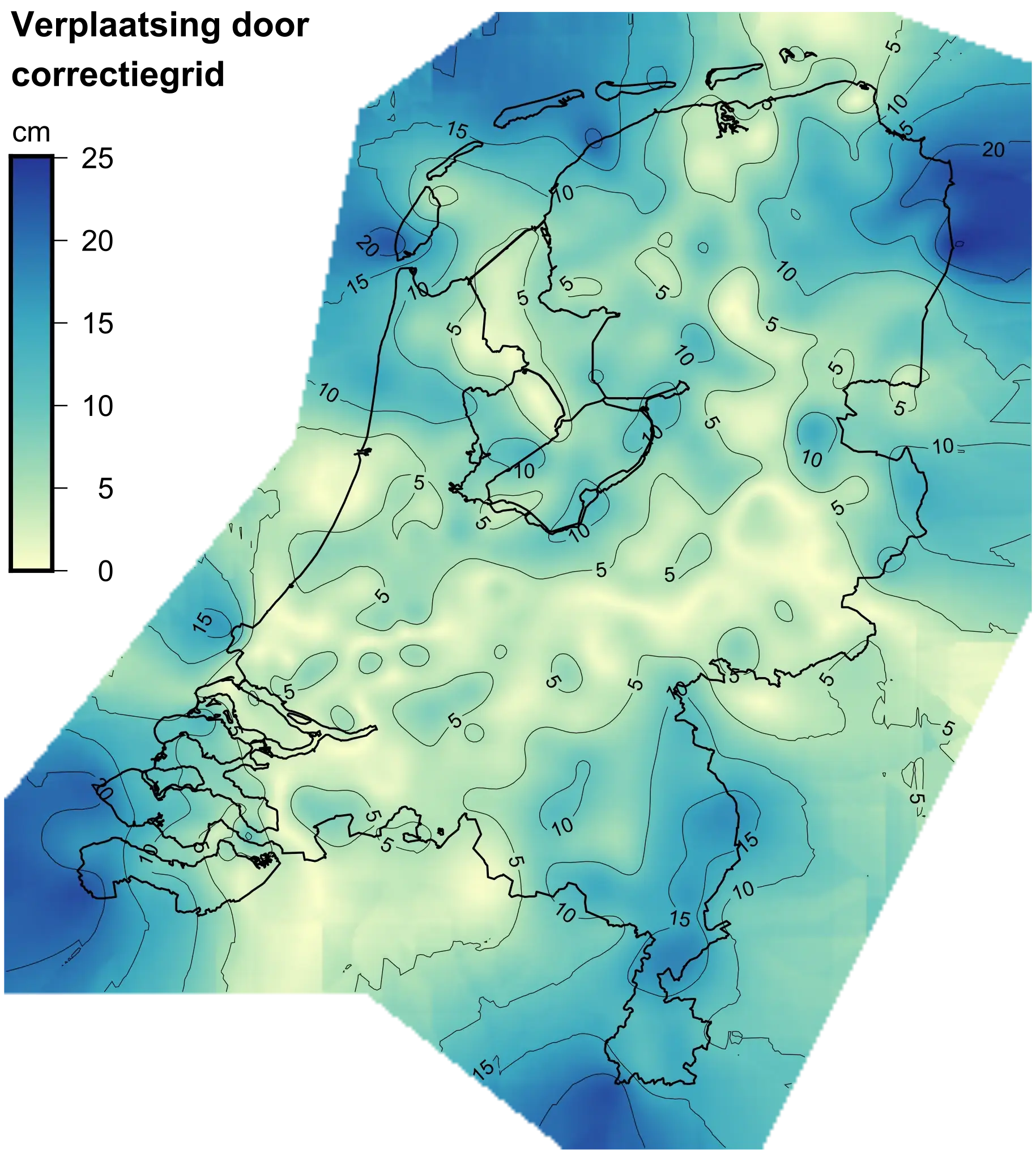
Het antwoord ligt in de lokale precisie. GPS werkt wereldwijd, maar het Rijksdriehoekstelsel is specifiek ontworpen voor Nederland. Het houdt rekening met de specifieke vorm van de aarde ter plaatse, lokale geologische verschuivingen en zelfs met bodemdaling door gaswinning.

GPS-coördinaten zijn gebaseerd op een ideale ellipsoïde – een perfect gladde, wiskundige benadering van de aardbol. Maar de werkelijke aarde (de geoïde) is grillig, met dalen en heuvels. In Nederland kan het verschil tussen de GPS-ellipsoïde en de werkelijkheid oplopen tot meters!

Het RD-stelsel is daarentegen gekalibreerd op de échte vorm van Nederland. Het resultaat? Voor precisiewerk binnen onze landsgrenzen zijn RD-coördinaten betrouwbaarder en nauwkeuriger dan onbewerkte GPS-coördinaten.

Converteren: van GPS naar RD en terug

Nu we weten waarom beide systemen bestaan, ontstaat de vraag: hoe vertaal je tussen beide? Dit is waar complexe wiskunde om de hoek komt kijken.

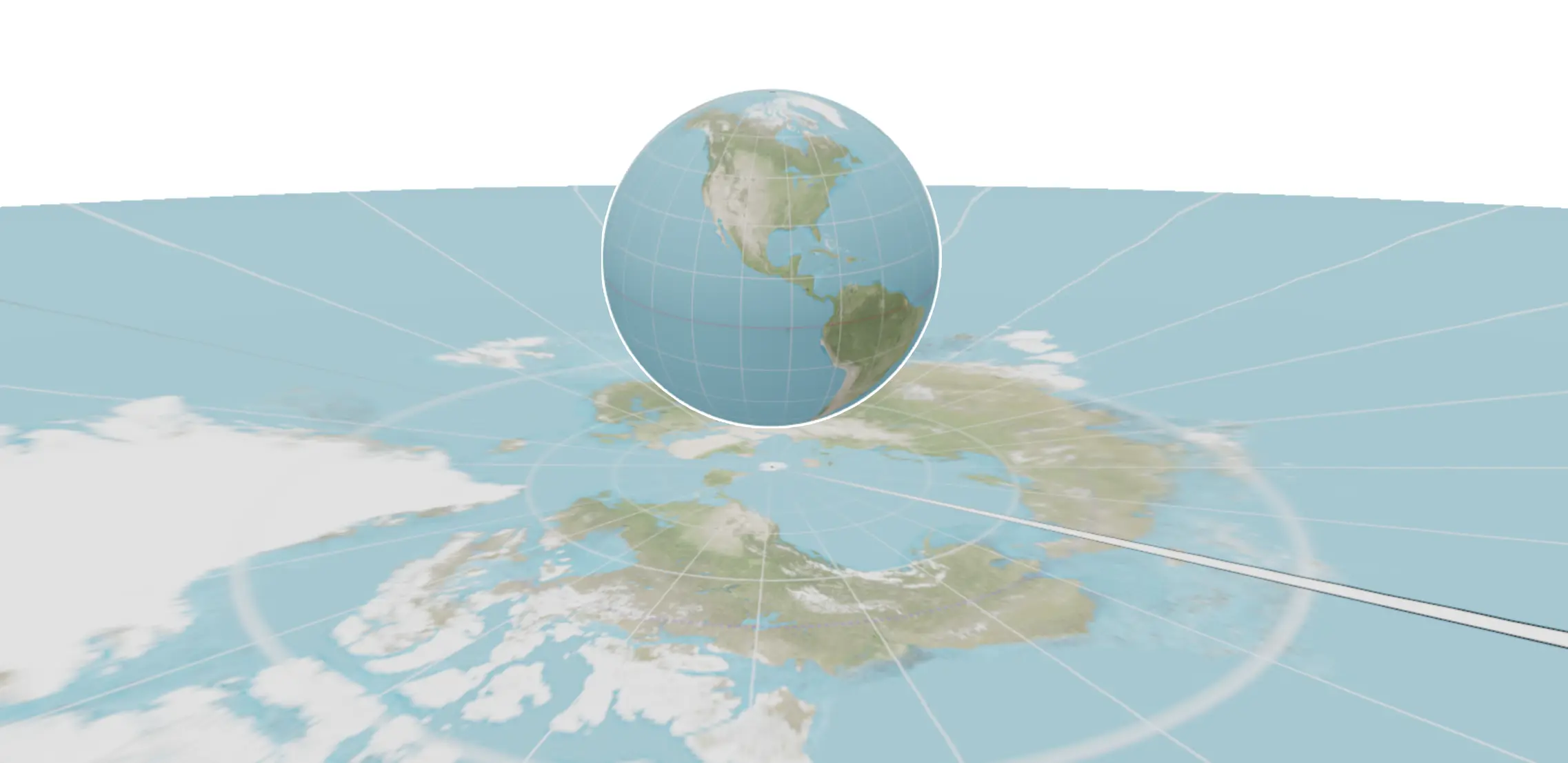
Het proces heet 'projectie', en het is vergelijkbaar met het proberen een sinaasappelschil plat op tafel te leggen – dat kan niet zonder te scheuren of te vervormen. Voor Nederland gebruiken we de 'stereografische projectie': stel je voor dat er een lamp in het middelpunt van de aarde zit, die alle punten op het aardoppervlak projecteert op een plat vlak dat Nederland raakt.

De formules (voor de dapperen)

Voor wie het echt wil weten, hier is een conceptuele weergave van de transformatie.

Wiskunde komt hier

Waar ϕ de breedtegraad is, λ de lengtegraad, en Kpq​ en Lpq​ vooraf berekende coëfficiënten zijn. Let op: dit is een vereenvoudigde weergave. In werkelijkheid is de officiële transformatie (RDNAPTRANS™) nog complexer en maakt deze gebruik van een grid met correctiewaarden om de hoogste nauwkeurigheid te garanderen.

De toekomst: wat komt er na RD?

De fundamenten van het Rijksdriehoekstelsel zijn nu meer dan 200 jaar oud, hoewel het moderne systeem zelf dateert uit de vroege 20e eeuw. Gaat het ooit vervangen worden? Waarschijnlijk niet binnenkort. Het stelsel is zo diep geworteld in de Nederlandse infrastructuur dat vervanging praktisch onmogelijk is.

Wel wordt het systeem voortdurend verfijnd. Moderne technieken zoals GNSS (het overkoepelende systeem van o.a. GPS) worden gebruikt om het stelsel nog nauwkeuriger te maken. En met technieken als RTK (Real-Time Kinematic) kunnen we nu relatieve nauwkeurigheden bereiken van enkele centimeters.

De kracht van precisie

Waarom maakt dit allemaal uit? In een land als Nederland, waar elke vierkante meter telt, is precisie essentieel. Of het nu gaat om het plaatsen van windmolens op zee, het aanleggen van nieuwe wijken, of het beschermen tegen overstromingen – alles begint met het exact weten waar je bent.

Het Rijksdriehoekstelsel is meer dan alleen een coördinatenstelsel: het is de onzichtbare basis onder onze hele samenleving. Van je huisadres tot de navigatie in je auto, van de plaatsing van verkeerslichten tot de grenzen van natuurgebieden – alles is gebaseerd op die nauwkeurige coördinaten die hun oorsprong vinden in de visionaire meetcampagnes van meer dan twee eeuwen geleden.

Zelf aan de slag

Nieuwsgierig geworden naar je eigen coördinaten? Het converteren tussen GPS en RD is complex, maar gelukkig hoef je de formules niet zelf uit te voeren. Rijksdriehoek.nl biedt tools om moeiteloos tussen beide stelsels wisselen.

Want uiteindelijk, of je nu werkt met 52.3676° N, 4.9041° E of met 121.538, 487.548 – je bent op dezelfde plek. Het verschil zit hem in hoe nauwkeurig en eenduidig je weet waar die plek precies is.

Het Rijksdriehoekstelsel: twee eeuwen nauwkeurigheid, gebouwd op de fundamenten van Franse ambitie en Nederlandse precisie.